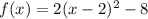Answer:
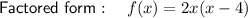
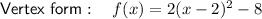
Explanation:
Factored form of a quadratic function
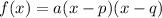
where:
- p and q are the x-intercepts
- a is some constant
Given x-intercepts:
Therefore:
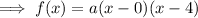
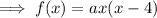
To find a, substitute the given vertex (2, -8) into the equation and solve for a:
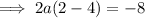
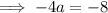
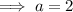
Therefore, the function's equation in factored form is:
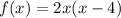
Vertex form of a quadratic equation
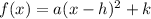
where:
- (h, k) is the vertex
- a is some constant
Given:
Therefore:
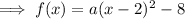
To find the constant a, substitute one of the x-intercepts into the equation and solve for a:
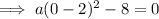
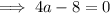
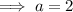
Therefore, the function's equation in vertex form is: