Question

Select the correct answer.
What are the zeros of the function y = x(x-2XX+6)²?

Answer 1

Finding the Zeros of a Polynomial Function

The zero product property tells us that if the product of two terms is 0, then one of the terms must be equal to 0.

Polynomial functions can be written in intercept form:

`y=x(x-r)(x-s)(...)`

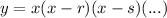
In this form, according to the zero product property, r and s are zeros of the function. The first 'x' term also signifies that 0 is also a zero of the function (x = 0).

Solving the Question

We're given:

`y=x(x-2)(x+6)^2`

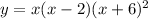
In this case, r and s are equal to 2 and -6.

• 2 and -6 are zeros of the function.

However, there is an x written in the front, indicating that 0 is also a zero of the function.

• 0 is a zero of the function.

Answer

-6, 0 and 2