The metal = Platinum(Pt)
Further explanation
FCC : Face centered cubic : the unit structures of the unit cell((other than BCC, HCP)
In FCC ⇒ atoms on every corner and side (total 4 atoms)
The length of the face diagonal (b) = 4 times the atomic radius (r)
Formula :
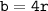
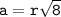
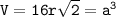
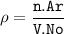
Ar = atomic mass, g/mol
No = Avogadro number = 6.02.10²³
n = number of atoms
V = volume (cm³)
a = side length
b = diagonal of the side surface
r = atomic radius
a= 392 pm=3.92 x 10⁻⁸ cm
ρ = 21.45 g/cm³
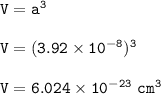
The atomic mass :
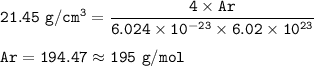
radius :
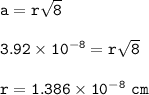
Element with atomic mass 195 g/mol and radius = 139 pm (1.386x10⁻⁸cm) = Platinum(Pt)