Answer:
See below
Explanation:
SAS requires two sides and the included angle to be congruent
Steve needs to measure sides EK and AC and if they are congruent, he can then complete his proof
Let's find the measure of EK and AC
- EC =
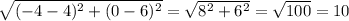
- AC =
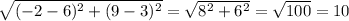
As we see EK = AC = 10, so the proof is complete