Question

At which value(s) of x does the graph of the function F(x) have a vertical asymptote? Check all that apply. F(x) = (x-4)(x + 2)

A. X= 4
B. X = 2
C. x= 1 n
D. x= -4
E.x= -2
F. x=0​

Answer 1

Answer: A and E.

Explanation:

For a function of the form:

F(x) = h(x)/g(x)

It only has a vertical asymptote in the points where the denominator is equal to zero, this means that we must have g(x) = 0.

In this case, we have:

F(x) = (x-4)(x + 2)

As this function has no denominator, this will not have any vertical asymptote, then i suppose that the actual function is:

`F(x) = (1)/((x - 4)*(x + 2))`

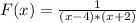
Using the same notation as above, we have:

g(x) = (x - 4)*(x + 2)

Then the vertical asympotes of F(x) will be on the values of x such that:

g(x) = 0.

As g(x) is already written in factorized form, we know that the zeros will be at the values of x that make one of the terms inside the parentheses equal to zero, these values are:

x = 4:

g(4) = (4 - 4)*(4 + 2) = (0)*6 = 0

and at x = -2

g(-2) = (-2 - 4)*(-2 + 2) = -6*0 = 0

Then the two asymptotes of F(x) are at x = 4, and x = -2

The correct options are:

A and E.