Question

1. Name the formula for the Law of Sines? Can it be written any other way? What do the letters stand for? When you are solving triangles, what information would be required in order to use the Law of Sines?

2. Name the formula for the Law of Cosines? Can it be written any other way? What do the letters stand for? When solving triangles, what information would be required in order to use the Law of Cosines?

3. When you have a 90-degree angle in a triangle, what happens to the Law of Cosines? What formula does it "turn in to?"

Answer 1

see explanation

Step-by-step explanation:

The formula for the Sine rule is

`(a)/(sinA)` =
`(b)/(sinB)` =
`(c)/(sinC)`

Where a, b and c are the sides of a triangle and A, B , C are the angles opposite the corresponding sides, that is

A is opposite side a, B is opposite side b, C is opposite side c

The sine rule is usually applied using a pair of the ratios, where

2 sides and an angle are known to find an unknown angle.

1 side and 2 angles are known to find an unknown side.

----------------------------------------------------------------------------------

2

There are 2 forms of the Cosine rule

(a) a² = b² + c² - (2bc cosA ) ← to calculate an unknown side

(b) cosA =
`(b^2+c^2-a^2)/(2bc)` ← to calculate an unknown angle

(a) is used given 2 sides of a triangle b and c are known with A being the included angle ( the angle between the 2 sides )

(b) is used when the 3 sides a, b and c are known

----------------------------------------------------------------------------------

3

If the angle A = 90° then cos90° = 0 and formula (a) becomes

a² = b² + c² ← that is Pythagoras' identity

Answer 2

9514 1404 393

Step-by-step explanation:

1. The Law of Sines says each side length is proportional to the sine of the opposite angle. As with any proportion, it can be written four ways. Corresponding parts can be numerators, denominators, or parts of the same ratio.

Where a, b, c are the side lengths, and A, B, C are the respective opposite angles, some of the formulations are ...

`(\sin(A))/(a)=(\sin(B))/(b)=(\sin(C))/(c)\\\\(a)/(\sin(A))=(b)/(\sin(B))=(c)/(\sin(C))\\\\(a)/(b)=(\sin(A))/(\sin(B))\quad (a)/(c)=(\sin(A))/(\sin(C))`

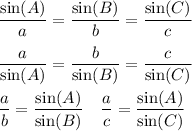
When solving triangles, you need ...

• at least one angle and its opposite side, and
• any other angle or side.

__

2. The Law of Cosines is conventionally written as ...

`c^2=a^2+b^2-2ab\cos(C)`

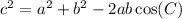
where c is the side opposite angle C, and a and b are the sides bounding angle C. Any of the side and angle designations can be interchanged, so, for example, it can also be written ...

`a^2=b^2+c^2-2bc\cos(A)`

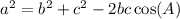
The equation can be solved for the angle, which gives ...

`A=\arccos{\left((b^2+c^2-a^2)/(2bc)\right)}`

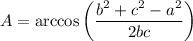
When using this formula, you need ...

• two sides and one angle, or
• three sides

If the two given sides do not bound the given angle, the Law of Sines may be easier to use. Using the Law of Cosines will result in a quadratic equation for the unknown side, whereas the Law of Sines will give a linear equation.

__

3. When the enclosed angle is a right angle, the Law of Cosines degenerates to a statement of the Pythagorean theorem. (The cosine term vanishes.)