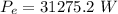Question

A heat engine has three quarters the thermal efficiency of a carnot engine operating between temperatures of 65°C and 435°C if the heat engine absorbs heat at a rate of 44.0 kW, at what rate is heat exhausted?

Answer 1

The value is
`P_e = 31275.2 \ W`

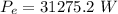
Step-by-step explanation:

From the question we are told that

The efficiency of the carnot engine is
`\eta`

The efficiency of a heat engine is
`k = (3)/(4) * \eta`

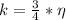
The operating temperatures of the carnot engine is
`T_1 = 65 ^oC =338 \ K` to
`T_2 = 435 ^oC = 708 \ K`

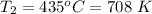
The rate at which the heat engine absorbs energy is
`P = 44.0 kW = 44.0 *10^(3) \ W`

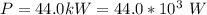
Generally the efficiency of the carnot engine is mathematically represented as

`\eta = [ 1 - (T_1 )/(T_2) ]`

=>
`\eta = [ (T_2 - T_1)/(T_2) ]`

=>
`\eta = 0.3856`

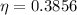
Generally the efficiency of the heat engine is

`k = (3)/(4) * 0.3856`

=>
`k = 0.2892`

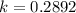
Generally the efficiency of the heat engine is also mathematically represented as

`k = (W)/(P)`

Here W is the work done which is mathematically represented as

`W = P - P_e`

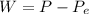
Here
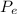`P_e` is the heat exhausted

So

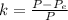
`k = (P - P_e)/(P)`

=>
`0.2892 = (44*10^(3) - P_e)/(44*10^(3))`

=>
`P_e = 31275.2 \ W`