Question

A T-shirt cannon can shoot a 0.085 kg T-shirt at nearly 30 m/s. The T-shirt cannon has a mass of 33 kg. If the initial net momentum is at 0 then what is the velocity of the recoil of the T-shirt cannon?

Answer 1

Approximately
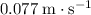`0.077\; {\rm m\cdot s^(-1)}` (assuming that external forces on the cannon are negligible.)

Step-by-step explanation:

If an object of mass
`m` is moving at a velocity of
`v`, the momentum
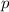`p` of that object would be
`p = m\, v`.

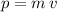Momentum of the t-shirt:

`\begin{aligned} p(\text{t-shirt}) &= m(\text{t-shirt}) \, v(\text{t-shirt}) \\ &= 0.085\; {\rm kg} * 30\; {\rm m \cdot s^(-1)} \\ &= 2.55 \; {\rm kg \cdot m \cdot s^(-1)} \end{aligned}`.

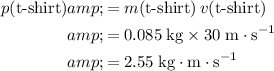If there is no external force (gravity, friction, etc.) on this cannon, the total momentum of this system should be conserved. In other words, if
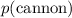`p(\text{cannon})` denote the momentum of this cannon:

`p(\text{t-shirt}) + p(\text{cannon}) = 0`.

`p(\text{cannon}) = -p(\text{t-shirt}) = -2.55\; {\rm kg \cdot m \cdot s^(-1)}`.

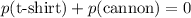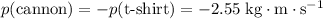Rewrite
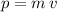`p = m\, v` to obtain
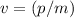`v = (p / m)`. Since the mass of this cannon is
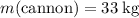`m(\text{cannon}) = 33\; {\rm kg}`, the velocity of this cannon would be:

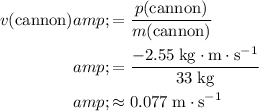`\begin{aligned} v(\text{cannon}) &= \frac{p(\text{cannon})}{m(\text{cannon})} \\ &= \frac{-2.55\; {\rm kg \cdot m \cdot s^(-1)}}{33\; {\rm kg}} \\ &\approx 0.077\; {\rm m \cdot s^(-1)}\end{aligned}`.