Question

Which of the following describes the end behavior of the function below?

Answer 1

2 Answers:

As
`x \to \infty, \ f(x) \to -\infty`

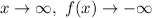
As
`x \to -\infty, \ f(x) \to \infty`

==================================================

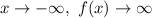
Step-by-step explanation:

The degree of this polynomial is the largest exponent. In this case, the degree is 9.

The degree being an odd number means that the end behavior has one end going up and the other end going down. The ends go in opposite directions.

As we move to the right, the curve goes downhill. We can say the curve "falls to the right". This is due to the fact that the leading coefficient is negative.

On the flip side, as we move to the left, the curve goes uphill. We can say the curve "rises to the left".

The graph below indicates these features. In this case, I chose b = 1 and c = 1. It turns out these values do not affect the answers mentioned at the top. The end behavior will be the same for any real numbers b and c. This is because the leading term -x^9 dictates entirely what the end behavior will be.

Answer 2

It is an odd-degree polynomial. Therefore...

As the coefficient is negative for x^9.

When x < 0 or x approaches negative infinity, y or f(x) will approach positive infinity.

When x approaches positive infinity, y or f(x) will approach negative infinity.

So it is the second and the third.