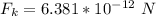Complete Question
Electromagnetic radiation from a 3.00 mW laser is concentrated on a 2.00 mm2 area. Suppose a 6.00 nC electric charge is in the beam. What is the maximum electric force (in N) it experiences? If the static charge moves at 300 m/s, what maximum magnetic force (in N) can it feel?
Answer:
The value are
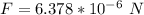
and
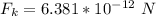
Step-by-step explanation:
From the question we are told that
The power of the laser is
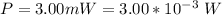
The area is
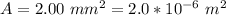 ]
]
The speed is
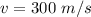
The magnitude of the electric charge is

Generally the intensity of the beam is mathematically represented as

=>
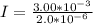
=>
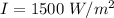
Generally the magnitude of the electric field is mathematically represented as
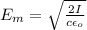
Here c is the speed of light with value
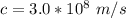
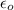 is the permittivity of free space with value
is the permittivity of free space with value
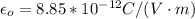
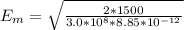
=>
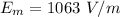
Generally the maximum electric force is mathematically represented as
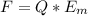
=>
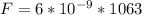
=>
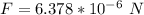
Generally the intensity of the beam can also be mathematically represented as
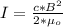
Here B is the magnetic field
 is the permeability of free space with value
is the permeability of free space with value
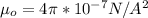
So
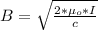
=>
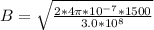
=>
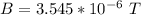
Generally the maximum magnetic force is mathematically represented as
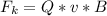
=>
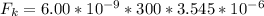
=>