Answer:
Explanation:
Suppose u = i + j =
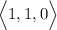 & v = j + k =
& v = j + k =
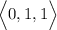
The direction vector for the line u*v is:
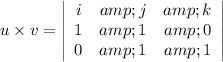
= (1-0) i - (1 - 0)j + ( 1- 0) k
= i - j - k
=
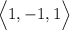
Hence, the equation of the line via the point (5,4,0 ) and the direction vector
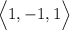 is as follows:
is as follows:
r(t) = (5,4,0) + t
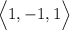
r(t) = (5+t, 4-t, t)
The symmetric equations of the line are:
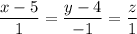
x - 5 = -(y-4) = z
The parametric equation of the line is:

x = 5 + t , y = 4 - t , z = t