Question

A 5 foot tall person walks away from a 12 foot tall lamppost at a constant rate of 4 feet per second. What is the rate that the tip of the shadow moves away from the lamppost when the person is 9 feet away from the pole?

Answer 1

Given :

The height of the person is 5 foot.

The height of the lamppost is 12 foot.

Speed of the person away from the lamppost = 4 ft/s

Let the distance of the tip of the shadow of the perosn to the pole at t seconds after the person started walking away from the pole be d(t).

By similarity of the triangles, we see that

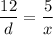`$(12)/(d)=(5)/(x)$` .................(i)

Here x is the distance from the person to the tip of the shadow. As it is given the speed of the person is 4 ft/s, then the distance of the person from the pole 4t. So we have,

x = d - 4t .............(ii)

Putting (ii) in (i) and solving for d is

d(t) = 6.85 t

So now if we derive d(t), we will get the wanted rate of the tip of the shadow.

∴ d'(t) = 6.85 ft/s