Answer:
The dimension that minimizes the container is width = 1; base = 2 and height = 5
The minimum cost is $36
Step-by-step explanation:
Let the width be x
So:
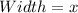
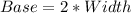
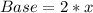
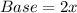

Volume of the box is:
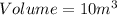 ---- Given
---- Given
Volume is calculated as:

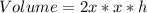

Substitute 10 for Volume

Make h the subject
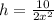
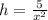
Next, we calculate area of the sides.
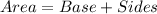
Because it has an open top, the area is:

![Sides\ Area = 2[(Width * Height) + (Base * Height)]](https://img.qammunity.org/2021/formulas/business/college/7ywe6zjk33j76riwu1z5nbpjflfo500sjg.png)
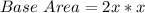
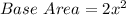
![Sides\ Area = 2[(Width * Height) + (Base * Height)]](https://img.qammunity.org/2021/formulas/business/college/7ywe6zjk33j76riwu1z5nbpjflfo500sjg.png)
![Side\ Area = 2[(x * h) + (2x * h)]](https://img.qammunity.org/2021/formulas/business/college/adr8t8u8t487xd2g71absnby2d7ja0by5p.png)
![Side\ Area = 2[(xh) + (2xh)]](https://img.qammunity.org/2021/formulas/business/college/aus97n57mw85h50fvq3ex0sved0h4r3nxr.png)
![Side\ Area = 2[3xh]](https://img.qammunity.org/2021/formulas/business/college/v1q8v09de216yjbe0mma1avinxjtyj1wo1.png)

The base area costs $6 per m²
So, the cost of 2x² would be:
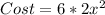
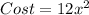
The side cost area costs $0.8 per m²
So, 6xh would cost
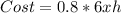
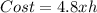
Total Cost (C) is:

Recall that
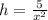
So:
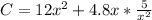



Take derivative of C

Take LCM
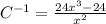
Equate
 to 0
to 0
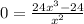
Cross multiply
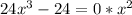
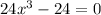
Add 24 to both sides

Divide through by 24
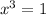
Take cube roots of both sides

Recall that
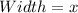
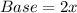
 and
and
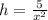
Solve for these dimensions:
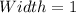
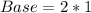


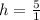
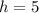
i.e.
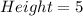
Hence, the dimension that minimizes the container is width = 1; base = 2 and height = 5
Recall that

Substitute 1 for x
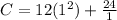

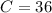
The minimum cost is $36