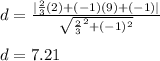Question

A house is built on coordinates (2,9). There is a water pipeline that runs along the line y = 2 3 x – 1. What is the approximate shortest length of new pipeline needed to connect the house to the existing pipeline?

Answer 1

7.21 units

Explanation:

The shortest length needed to connect the house to the existing pipeline is the perpendicular distance between the location of the house (2,9) and the line y = 2/3x - 1.

The perpendicular distance (d) between a point (
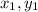`x_1,y_1`) and the line Ax + By + C = 0 is given as:

`d=(|Ax_1+By_1+C|)/(√(A^2+B^2) )`

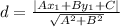
The line is given by y = 2/3 x - 1; 2/3x - y - 1 = 0. The point = (2, 9)

hence A = 2/3, B = -1, C = -1,
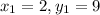`x_1=2,y_1=9\\`. Therefore:

`d=\frac{\sqrt{(2)/(3)^2+(-1)^2 } } \\\\d=7.21`