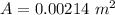Question

500 nm light passes through a circular aperture that has a diameter d = 30.0 μm. A diffraction pattern forms on a screen 350 mm from the aperture. Calculate the area of the central bright fringe.

Answer 1

Complete Ques

Answer:

The value is
`A = 0.00214 \ m^2`

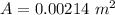
Step-by-step explanation:

From the question we are told that

The wavelength is
`\lambda = 500 \ nm = 500 *10^(-9) \ m`

The diameter of the aperture is
`d = 30 \mu m = 30*10^(-6) \ m`

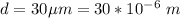
The distance of the screen from the aperture is
`D = 350 \ m m = 0.350 \ m`

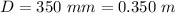
Generally the distance from the center the the edge of the central bright fringe is magmatically reparented as

`y = (m * \lambda * D)/(d)`

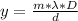
Generally m = 1 because after the central bright fringe we have the first order fringe

So

`y = (1 * 500 *10^(-9) * 0.350)/(30*10^(-6))`

=>
`y =0.00583 \ m`

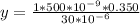
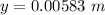
Generally the area of the central bright fringe

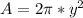
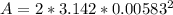
`A = 2 \pi * y^2`

=>
`A = 2 * 3.142 * 0.00583^2`

=>
`A = 0.00214 \ m^2`