Question

g Bonus: Assume that among the general pediatric population, 7 children out of every 1000 have DIPG (Diffuse Intrinsic Pontine Glioma, an aggressive brain cancer). A pharmaceutical company designs a screening test for DIPG that has a 98% sensitivity and an 84% specificity. Given that someone has a positive test result, what is the probability they don't have DIPG

Answer 1

0.9586

Explanation:

From the information given:

7 children out of every 1000 children suffer from DIPG

A screening test designed contains 98% sensitivity & 84% specificity.

Now, from above:

The probability that the children have DIPG is:

`\mathbf \ not \DIPG)* P(not \ DIPG)`
`= 0.98\imes( (7)/(1000)) + (1-0.84) * (1 - (7)/(1000))`

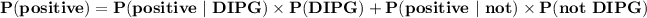
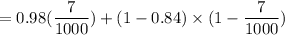
= (0.98 × 0.007) + 0.16( 1 - 0.007)

= 0.16574

So, the probability of not having DIPG now is:

`P(not \ DIPG \ | \ positive) = \frac \ not DIPG)*P(not \ DIPG) { P(positive)}`

`=( (1-0.84)* (1 - (7)/(1000)) )/( 0.16574)`

`=( 0.16 ( 1 - 0.007) )/(0.16574)`

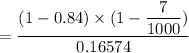
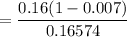
= 0.9586