Question

A random sample of size 64 was obtained which had sample mean of 1.03 and sample standard deviation of 0.189. Find the P-value.

Answer 1

The P-value is 80.23%

Explanation:

Given;

number of samples, n = 64

sample mean, X = 1.03

standard deviation, σ = 0.189

`sample \ mean \ (X) = (Sum \ of \ samples)/(number \ of \ samples \ -1) \\\\1.03 = (Sum \ of \ samples)/(64 -1)\\\\Sum \ of \ samples = 1.03(63)\\\\Sum \ of \ samples = 64.89`

Population mean (μ) is given as;

`\mu = (Sum \ of \ samples)/(number \ of \ samples) \\\\\mu = (64.89)/(64) \\\\\mu = 1.01 \\`

The z-score is given as;

`z = (X -\mu)/((\sigma)/(√(n) ) )\\\\z = (1.03 -1.01)/((0.189)/(√(64) ) )\\\\z = (0.02)/((0.189)/(8) )\\\\z = 0.8466 \\`

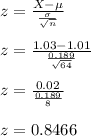
z ≅ 0.85

From the z-table, the P-value at the given z-score is 0.8023 = 80.23%;