Question

What is the determinant ?
ANS : -2
plz help me with process​

Answer 1

(-2)

Explanation:

We have to find the determinant of the given matrix,

`A=\begin{bmatrix}(a-1) & (a^2-a+1)\\ (a+1) & (a^2+a+1)\end{bmatrix}`

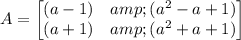
det A = (a - 1)(a² + a + 1) - (a + 1)(a² - a + 1)

= a(a² + a + 1) - 1(a²+ a + 1) - a(a² - a + 1) - 1(a² - a + 1)

= a³ + a² + a - a² - a - 1 - a³ + a² - a - a² + a - 1

= (a³ - a³) + (-a² + a² - a² - a²) - 1 - 1

= -2

Therefore, determinant of the given matrix is (-2).