Question

An element with a mass of 990 grams decays by 16.9% per minute. To the nearest Minute, how lon will it be until there are 80 grams of the element remaining?

Answer 1

It will take approximately 246 minutes for the element to decay to 80 grams.

Step-by-step explanation:

To determine how long it will take for the element to decay to 80 grams, we can set up a decay equation using the given information. We have an initial mass of 990 grams and a decay rate of 16.9% per minute. Let's denote the time it takes for the mass to decay to 80 grams as t.

Using the formula for exponential decay, we can write the equation as:

`990 * (1 - 0.169)^t = 80`

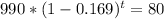
Simplifying the equation:

`(0.831)^t = 80/990`

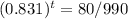
Taking the natural logarithm of both sides

t * ln(0.831) = ln(80/990)

Dividing both sides by ln(0.831):

t = ln(80/990) / ln(0.831)

Using a calculator, we find t to be approximately 246 minutes.

Therefore, it will take approximately 246 minutes for the element to decay to 80 grams.