Answer:

Explanation:
See attachment for graph
Required
Determine the domain of Emma's line
First, we calculate the equation of Emma's line
Start by calculating the slope (m)
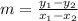
Where the x's and y's represent corresponding values of x and y on Emma's line
Emma's line is represented by the thick line.
So, we have:
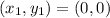
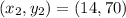
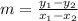 becomes
becomes

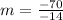

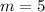
The equation is then calculated using:

Where
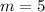
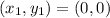
So:

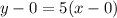
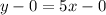
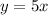
To get the domain, we have the following:
x represents time and x can not be negative.
So, the least value of x is: x = 0
The maximum value of x is unknown.
So, the maximum value of x is: x = +infinity
Hence, the domain is
