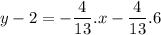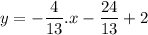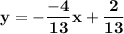Question

Given AABC with A(-9,-4), B(-3.8), and C(7.-2), complete the following: 7. Find the equation of CE median in point-slope form.​

Answer 1

`\displaystyle y=-(4)/(13)x+(2)/(13)`

Explanation:

Median of a Triangle

The median of a triangle is a line segment joining a vertex to the midpoint of the opposite side.

We have a triangle formed by the points A(-9,-4), B(-3.8), and C(7.-2).

The median from vertex C must pass through the midpoint of the segment AB. First, find that midpoint:

The midpoint (xm,ym) is calculated as follows:

`\displaystyle x_m=(x_1+x_2)/(2)=(-3-9)/(2)=-6`

`\displaystyle y_m=(-4+8)/(2)=2`

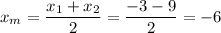
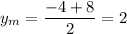
Midpoint AB=(-6,2). This point and C(7,-2) form the required median.

The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`\displaystyle y-2=(-2-2)/(7+6)(x+6)`

`\displaystyle y-2=-(-4)/(13)(x+6)`

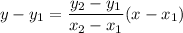
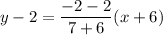
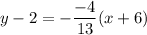
Operating:

`\displaystyle y-2=-(4)/(13).x-(4)/(13).6`

`\displaystyle y=-(4)/(13).x-(24)/(13)+2`

`\mathbf{\displaystyle y=-(-4)/(13)x+(2)/(13)}`