Given the differential equation
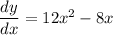
integrating both sides with respect to
 yields
yields
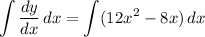

Use the given point to solve for the constant
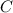 :
:
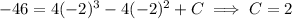
Then the equation of the curve is
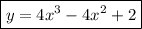
On the off-chance you instead meant something like
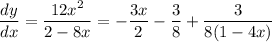
integrating would instead give
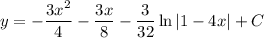
Then
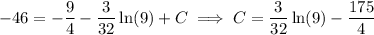
and the particular solution follows. (But I suspect this is *not* what you meant.)