Question

Which equation represents the line that is perpendicular to y = 5 and passes through (-4,-3)?

А.
x= -4
B.
x= -3
C. y=-5
D. y=-3

Answer 1

The required equation is: y=-3

Option D is correct.

Explanation:

We need to write equation of line that is perpendicular to y = 5 and passes through (-4,-3).

The equation of line in slope-intercept form is expressed as:
`y=mx+b`

where m is slope and b is y-intercept.

Finding Slope:

Comparing with the given equation y=5, the slope m =0

The slope of required line will be opposite reciprocal of 0 as both lines are perpendicular. so it will be m=0

Finding y-intercept

The y-intercept can be found using slope m=0 and point (-4,-3)

`y=mx+b\\-3=0(-4)+b\\b=-3`

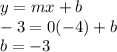
So, y-intercept b is b=-3

The equation of required line having slope m=0 and y-intercept b=-3 is

`y=mx+b\\y=0(x)-3\\y=-3`

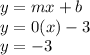
So, required equation is: y=-3

Option D is correct.