Answer:
50/65
Explanation:
we mark the width as w and the length as l
we know that:
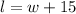
we also know the area of a rectangle is given by:
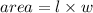
since the area is given, we substitute l and get:
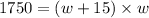
from this we derive the following quadratic equation:
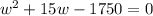
we aolve for w, using the quadratic formula:
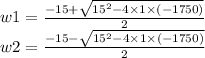
and finally:
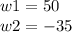
since the width cannot be a negative number, w1 is the width, hence 50 ft, and the length is 65ft