Question

A rectangular garden is 15 ft longer than it is wide. Its area is 1750 ft². What are its dimensions?

Answer 1

50/65

Explanation:

we mark the width as w and the length as l

we know that:

`l = w + 15`

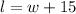
we also know the area of a rectangle is given by:

`area = l * w`

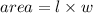
since the area is given, we substitute l and get:

`1750 = (w + 15) * w`

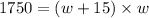
from this we derive the following quadratic equation:

`{w}^(2) + 15w - 1750 = 0`

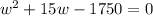
we aolve for w, using the quadratic formula:

`w 1 = \frac{ - 15 + \sqrt{ {15}^(2) - 4 * 1 * ( - 1750)} }{2} \\ w 2 = \frac{ - 15 - \sqrt{ {15}^(2) - 4 * 1 * ( - 1750)} }{2}`

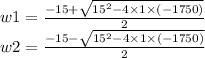
and finally:

`w1 = 50 \\ w2 = - 35`

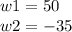
since the width cannot be a negative number, w1 is the width, hence 50 ft, and the length is 65ft