Given:
The equation of a line is
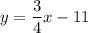
Line v passes through point (6,6) and it is perpendicular to the given line.
Line w passes through point (-6,10) and it is parallel to the line v.
To find:
The equation in slope intercept form of line w.
Solution:
Slope intercept form of a line is
 ...(i)
...(i)
where, m is slope and b is y-intercept.
We have,
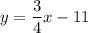 ...(ii)
...(ii)
On comparing (i) and (ii), we get
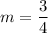
So, slope of given line is
 .
.
Product of slopes of two perpendicular lines is -1.
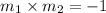
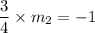

Line w is perpendicular to the given line. So, the slope of line w is
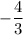 .
.
Slopes of parallel line are equal.
Line v is parallel to line w. So, slope of line v is also
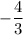 .
.
Slope of line v is
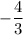 and it passes thorugh (-6,10). So, the equation of line v is
and it passes thorugh (-6,10). So, the equation of line v is

where, m is slope.
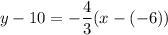
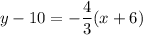
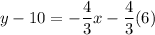
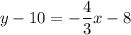
Adding 10 on both sides, we get
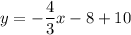
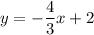
Therefore the equation of line v is
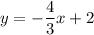 .
.