Question

A 1.5-kg mass attached to an ideal massless spring with a spring constant of 20.0 N/m oscillates on a horizontal, frictionless track. At time t = 0.00 s, the mass is released from rest at x = 10.0 cm. (That is, the spring is stretched by 10.0 cm.)Express the displacement x as a function of time t.

Answer 1

x = 0.100 cos (3.65 t)

Step-by-step explanation:

We must solve Newton's second law for this case

F = m a

the spring force is given by Hooke's law

F = -kx

and the definition of acceleration is

a =
`(d^2x)/(dt^2)`

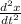
let's substitute

- kx = m \frac{d^2x}{dt^2}

\frac{d^2x}{dt^2} +
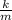`(k)/(m)` x = 0

this equation has as a solution

x = A cos (wt + Ф)

where

w =
`\sqrt{(k)/(m) }`

let's calculate

w =
`\sqrt{(20)/(1.5) }`

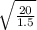
w = 3.65 rad / s

to find the constant fi let's use the condition t = 0 x = 10.0 cm

x = A cos (0 +Фi)

0.100 = A

therefore Ф = 0

the complete solution is

x = 0.100 cos (3.65 t)

this solution is in meters