Answer:
The location of the center of gravity of the fourth mass is
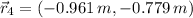 .
.
Step-by-step explanation:
Vectorially speaking, the center of gravity with respect to origin (
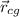 ), measured in meters, is defined by the following formula:
), measured in meters, is defined by the following formula:
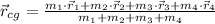 (1)
(1)
Where:
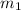 ,
,
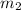 ,
,
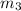 ,
,
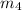 - Masses of the objects, measured in kilograms.
- Masses of the objects, measured in kilograms.
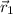 ,
,
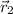 ,
,
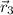 ,
,
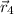 - Location of the center of mass of each object with respect to origin, measured in meters.
- Location of the center of mass of each object with respect to origin, measured in meters.
If we know that
![\vec r_(cg) = (0,0)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/2sozwq3c5milgy6jhpn0m86cakjdhf5458.png) ,
,
![\vec r_(1) = (0,0)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/7b68y5sipjj6hvuaj7y7v8e9co6jv6vjf5.png) ,
,
![\vec r_(2) = (0, 4.1)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/nqazvlhf88fh58ab9vknftm80dnjph1kn8.png) ,
,
![\vec r_(3) = (1.9,0.0)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/vq6lsq2rfpclyu82auiae1r5ypt5v6zpid.png) ,
,
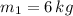 ,
,
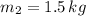 ,
,
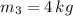 and
and
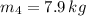 , then the equation is reduced into this:
, then the equation is reduced into this:
![(0,0) = ((6\,kg)\cdot (0,0)\,[m]+(1.5\,kg)\cdot (0,4.1)\,[m]+(4.0\,kg)\cdot (1.9,0)\,[m]+(7.9\,kg)\cdot \vec r_(4))/(6\,kg+1.5\,kg+4\,kg+7.9\,kg)](https://img.qammunity.org/2021/formulas/physics/college/uyy0hp0m4544s6u26ha8ww8kreyopvs9rc.png)
![(6\,kg)\cdot (0,0)\,[m]+(1.5\,kg)\cdot (0,4.1)\,[m]+(4\,kg)\cdot (1.9,0)\,[m]+(7.9\,kg)\cdot \vec r_(4) = (0,0)\,[kg\cdot m]](https://img.qammunity.org/2021/formulas/physics/college/tvrh8a2sq7jnmu925bss8vlnpjsdhlwtbk.png)
![(7.9\,kg)\cdot \vec r_(4) = -(6\,kg)\cdot (0,0)\,[m]-(1.5\,kg)\cdot (0,4.1)\,[m]-(4\,kg)\cdot (1.9,0)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/3j13ilmgocv80r47t1eysrt4inq3g5l2d9.png)
![\vec r_(4) = -0.759\cdot (0,0)\,[m]-0.190\cdot (0,4.1)\,[m]-0.506\cdot (1.9,0)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/urt1yn7594nebxz0qen258noq7ii5c58z9.png)
![\vec r_(4) = (0, 0)\,[m] -(0, 0.779)\,[m]-(0.961,0)\,[m]](https://img.qammunity.org/2021/formulas/physics/college/omnb8hs4n442wh7tvq7n64322lkuj6jg0u.png)
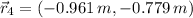
The location of the center of gravity of the fourth mass is
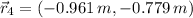 .
.