Question

For a group of 70 people, assuming that each person is equally likely to have a birthday on each of 365 days in the year, compute (a) The expected number of days of the year that are birthdays of exactly 4 people:

Answer 1

0.0157

Explanation:

From the information given:

The sample size = 70

The expected no. of days of year that are birthday of exactly 4 people is:
`P = \bigg [ (1)/(365) \bigg]^4`

The expected number of days with 4 birthdays =
`\sum \limits ^(365)_(i=1) E(x_i)`

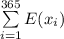
`\sum \limits ^(365)_(i=1) E(x_i) = 365 * \bigg[ \ ^(70)C_(4) * ( (1)/(365))^4 ( 1 - (1)/(365))^(70-4) \bigg]`

`\sum \limits ^(365)_(i=1) E(x_i) = 365 * \bigg[ \ (70!)/(4!(70-4)!) * ( (1)/(365))^4 ( 1 - (1)/(365))^(66) \bigg]`

`\sum \limits ^(365)_(i=1) E(x_i) = 365 * \bigg[ \ 916895 * 5.6342 * 10^(-11) * 0.8343768898 \bigg]`

= 0.0157

Therefore, the required probability = 0.0157