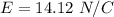Question

A long, nonconducting cylinder (radius = 12 cm) has a charge of uniform density (5.0 nC/m3) distributed throughout its column. Determine the magnitude of the electric field 5.0 cm from the axis of the cylinder.

Answer 1

The value is
`E = 14.12 \ N/C`

Step-by-step explanation:

From the question we are told that

The radius of the cylinder is
`r = 12 \ cm = 0.12 \ m`

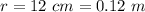
The density of the charge is
`\rho = 5.0 \ nC/m^3 = 5.0*10^(-9) \ C/m^3`

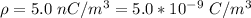
The position consider is a = 5.0 cm = 0.05 m

Gnerally from the magnitude of the magnetic field is mathematically represented as

`E = (\rho * s)/( 2 * \epsilon_o )`

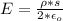
Here
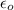`\epsilon_o` is the permittivity of free space with value
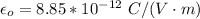
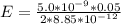
`\epsilon_o = 8.85 *10^(-12) \ C/(V \cdot m)`

=>
`E = (5.0*10^(-9) * 0.05)/( 2 * 8.85*10^(-12) )`

=>
`E = 14.12 \ N/C`