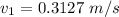Question

Sixty identical drippers, each with a hole of diameter 1.00 mm, are used to water a yard. If the water in the main pipe of diameter 2.54 cm is flowing at speed 3.00 cm/s, (a) how much water is used in one hour and (b) how fast the water is coming out the drippers

Answer 1

a

`V = 5.30 *10^(-2) \ m^3`

b

`v_1 = 0.3127 \ m/s`

Step-by-step explanation:

From the question we are told that

The number of identical drippers is n = 60

The diameter of each hole in each dripper is
`d = 1.0 \ mm = 0.001 \ m`

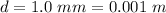
The diameter of the main pipe is
`d_m = 2.5 \ cm = 0.025 \ m`

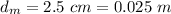
The speed at which the water is flowing is
`v = 3.00 \ cm/s = 0.03 \ m/s`

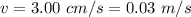
Generally the amount of water used in one hour = 3600 seconds is mathematically represented as

`V = A * v * 3600`

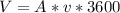
Here A is the area of the main pipe with value

`A = \pi * (d^2)/(4)`

=>
`A = 3.142 * (0.025^2)/(4)`

=>
`A = 0.0004909 \ m^2`

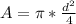
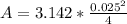
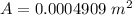
So

=>
`V = 0.0004909 * 0.03 * 3600`

=>
`V = 5.30 *10^(-2) \ m^3`

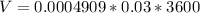
Generally the area of the drippers is mathematically represented as

`A_1= n * \pi (d^2)/(4)`

=>
`A_1 = 60 * 3.142 * (0.001 ^2)/(4)`

=>
`A_1 = 4.713 *10^(-5) \ m^2`

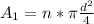
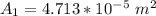
Generally from continuity equation we have that

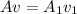
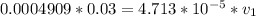
`Av = A_1 v_1`

=>
`0.0004909 * 0.03 = 4.713 *10^(-5) * v_1`

=>
`v_1 = 0.3127 \ m/s`