Answer:
A
Explanation:
For a quadratic equation in standard form:
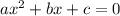
The discriminant, symoblized as Δ, is given by:
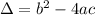
If:
- Δ>0 (positive), then our quadratic has two real roots.
- Δ<0 (negative), then our quadratic has no real roots. It does, however, have two imaginary (complex) roots.
- And if Δ=0 (zero), then our quadratic has exactly one real root.
We have the equation:
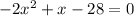
Thus:
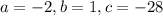
Substituting them for our discriminant:
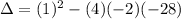
Evaluate:

Since our discriminant is negative, there is no real solutions.
Hence, our answer is A.