Question

Suppose you invest $2000 at annual interest rate of 4.5 % How much money do you have in the account after five years?

Round two decimal places.

compounded quarterly $ _____

compounded semi-annually $ _____

Answer 1

Please check the explanation.

Explanation:

To find the amount we use the formula:

`A=P\cdot \left(1+(r)/(n)\right)^(nt)`

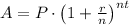
Here:

A = total amount

P = principal or amount of money deposited,

r = annual interest rate

n = number of times compounded per year

t = time in years

Given

P=$2000

r=4.5%

n=4

t = 5 years

Calculating compounded quarterly

After plugging in the values

`A=2000\left(1+(4.5\%\:)/(4)\right)^(4\cdot \:5)`

`A=2000\left(1+(0.045)/(4)\right)^(4\cdot \:5)`

`A=2000\cdot (4.045^(20))/(4^(20))`

`A=(125\cdot \:4.045^(20))/(2^(36))`

`A = 2,501.50`

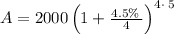
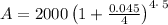
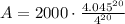
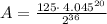
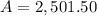
Thus, If you deposit $2000 into an account paying 4.5% annual interest compounded quarterly, you will have $2501.50 after five years.

Calculating compounded semi-annually

n = 2

`A=2000\left(1+(4.5\%\:)/(2)\right)^(2\cdot \:5)`

`A=2000\left(1+(0.045)/(2)\right)^(2\cdot \:5)`

`A=2000\cdot (2.045^(10))/(2^(10))`

`A = 2,498.41`

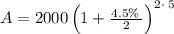
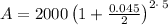
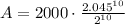
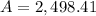
Thus, If you deposit $2000 into an account paying 4.5% annual interest compounded semi-annually, you will have $2,498.41 after five years.