Answer:
Please check the explanation
Explanation:
Given the function
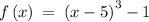
Given that the output = -3
i.e. y = -3
now substituting the value y=-3 and solve for x to determine the input 'x'
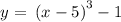
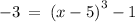
switch sides
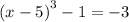
Add 1 to both sides
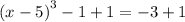
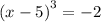
![\mathrm{For\:}g^3\left(x\right)=f\left(a\right)\mathrm{\:the\:solutions\:are\:}g\left(x\right)=\sqrt[3]{f\left(a\right)},\:\sqrt[3]{f\left(a\right)}(-1-√(3)i)/(2),\:\sqrt[3]{f\left(a\right)}(-1+√(3)i)/(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/zarma9zw16vsx08pd5qrr64v8nedjv7b98.png)
Thus, the input values are:
![x=-\sqrt[3]{2}+5,\:x=\frac{\sqrt[3]{2}\left(1+5\cdot \:2^{(2)/(3)}\right)}{2}-i\frac{\sqrt[3]{2}√(3)}{2},\:x=\frac{\sqrt[3]{2}\left(1+5\cdot \:2^{(2)/(3)}\right)}{2}+i\frac{\sqrt[3]{2}√(3)}{2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/bbg9by4gtghv0eah70k3g54wp4mw849afy.png)
And the real input is:
![x=-\sqrt[3]{2}+5](https://img.qammunity.org/2021/formulas/mathematics/high-school/ec49ahxw5au645fquwblnyeortxganc80k.png)