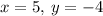Question

Solve this system of equations by graphing. First graph the equations, and then type the solution. 2x+5y=-10 and y=-3/5x-1

Answer 1

From the graph, it is clear that both lines intersect at x=5 and y=-4

Thus, the point of intersection is (x, y) = (5, -4)

(x, y) = (5, -4)

Please check the graph.

Explanation:

The solution graph is attached below.

From the attached solution graph,

• The red line is representing the equation 2x+5y=-10

• The blue line is representing the equation y=-3/5x-1

From the graph, it is clear that both lines intersect at x=5 and y=-4

Thus, the point of intersection is (x, y) = (5, -4)

Therefore, the point of intersection is the solution to the system of equations.

Hence, the solution is: (x, y) = (5, -4)

Please check the graph.

LET US SOLVE TO CHECK

`\begin{bmatrix}2x+5y=-10\\ y=-(3)/(5)x-1\end{bmatrix}`

`\mathrm{Arrange\:equation\:variables\:for\:elimination}`

`\begin{bmatrix}2x+5y=-10\\ (3)/(5)x+y=-1\end{bmatrix}`

`\mathrm{Multiply\:}2x+5y=-10\mathrm{\:by\:}3\:\mathrm{:}\:\quad \:6x+15y=-30`

`\mathrm{Multiply\:}(3)/(5)x+y=-1\mathrm{\:by\:}10\:\mathrm{:}\:\quad \:6x+10y=-10`

`\begin{bmatrix}6x+15y=-30\\ 6x+10y=-10\end{bmatrix}`

`6x+10y=-10`

`-`

`\underline{6x+15y=-30}`

`-5y=20`

`\begin{bmatrix}6x+15y=-30\\ -5y=20\end{bmatrix}`

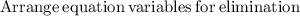
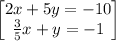
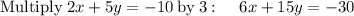
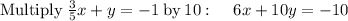
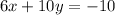
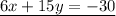
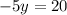
solve for y

`-5y=20`

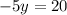
Divide both sides by -5

`(-5y)/(-5)=(20)/(-5)`

`y=-4`

`\mathrm{For\:}6x+15y=-30\mathrm{\:plug\:in\:}y=-4`

`6x+15\left(-4\right)=-30`

`6x-60=-30`

`6x=30`

`x=5`

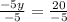
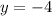
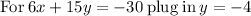
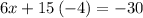
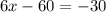
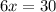
Thus, the solution is:

`x=5,\:y=-4`