Question

als den is 12 feet longer than it is wide. if the dens area is 405 square feet, what are the dimensions of the room?

Answer 1

The room has a length of 27 feet and width 15 feet.

Explanation:

Given that:

Area of den = A = 405 square feet

Let,

L represent the length of room and W represent the width of room.

L = W+12

Area = Length * Width

`405=(W+12)*W\\405=W^2+12W\\W^2+12W-405=0`

Factorizing the equation

`W^2-15W+27W-405=0\\W(W-15)+27(W-15)=0\\(W-15)(W+27)=0\\`

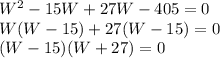
Either,

W-15 = 0

W=15

Or,

W+27=0

W=-27

As the width cannot be negative, therefore,

Width of den = 15 feet

Length of den = 15+12 = 27 feet

Hence,

The room has a length of 27 feet and width 15 feet.