Answer:
The solution is x = -2 and y = 2.
Explanation:
Given that:
14y - 8x = 44 Eqn 1
-7y = -x - 16 Eqn 2
In elimination method, you try to eliminate one variable in the equation by adding or subtracting.
Multiplying Eqn 2 by 2
2(-7y = -x - 16)
-14y=-2x-32
-14y+2x= -32 Eqn 3
Adding Eqn 1 and 3
(14y-8x)+(-14y+2x)=44+(-32)
14y-8x-14y+2x=44-32
-6x=12
Dividing both sides by -6
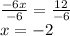
Putting x=-2 in Eqn 2
-7y=-(-2)-16
-7y=2-16
-7y=-14
Dividing both sides by -7

Hence,
The solution is x = -2 and y = 2.