-------------------------------------------------------------------------------------------------------------
Answer:
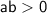
-------------------------------------------------------------------------------------------------------------
Given:

Find:
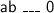
Solution: Since we know both a and b are positive this means that if they are multiplied against each other they would produce another positive. Therefore, this would cause the statement to be ab > 0.