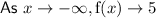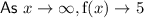Answer:
Asymptotes
x = 25, y = 5
End behavior
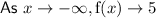
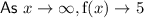
Explanation:
Given rational function:
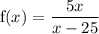
Asymptotes
An asymptote is a line that the curve gets infinitely close to, but never touches.
Vertical Asymptotes
To find the vertical asymptote(s) of a rational function, set the denominator to zero and solve for x.

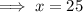
Horizontal Asymptotes
If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote (but there is a slant asymptote).
If the degree of the numerator is equal to the degree of the denominator, divide the highest degree term of the numerator by the highest degree term of the denominator.
As the degree of the numerator of the given function is equal to the degree of the denominator of the given function, the horizontal asymptote is:

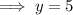
End Behavior
The end behavior of a function describes the behavior of the curve as x approaches positive and negative infinity.
As the given function has a horizontal asymptote at y = 5, this is the end behavior of the function. So as x approaches both positive and negative infinity, the function approaches the horizontal asymptote y = 5.