Question

if one root of a quadratic equation 6 x square minus KX + 48 is equal to zero is the square of the other find the roots and ends find the value of k​

Answer 1

value of k is ± 24√2

Decimal form: -33.94, 33.94

Explanation:

⇒ The given equation
`6x^(2) -kx +48=0`

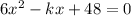
⇒ To find, The value of k if the roots are equal and real.

⇒ Solution,We can easily solve this problem by following the given steps.

According to the question,

We have the following quadratic equation:
`6x^(2) -kx +48=0`

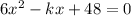
Now, we know that if the roots are real and equal then the value of the determinant (D) is zero.

D =
`\sqrt{b^(2) - 4ac}` = 0

b² = 4ac

b² - 4ac = 0

Here, a = 6, b = -k, c = 48

⇒ (-k)² − 4(6)(48) = 0

⇒ k² − 24(48) = 0

⇒ k² − 1,152 = 0

⇒ k² − 1,152 + 1,152 = 0 + 1,152

⇒ k² = 1,152

⇒ k =√1,152

⇒ k = ±24√2

Hence, the value of k is ± 24√2