QUESTION:
Solve the following equation 2/3 x + 6 = 1/2 x + 1/4x
ANSWER:
In all choices the correct answer is B

STEP-BY-STEP Step-by-step explanation:
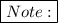 Since x is on the right side of the equation, switch the sides so it is on the left side of the equation
Since x is on the right side of the equation, switch the sides so it is on the left side of the equation
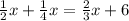
First, Simply each term
Combine
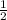 ,
,
 to x
to x
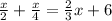
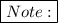 To write
To write
 as a fraction with a common denominator, multiply by
as a fraction with a common denominator, multiply by
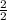
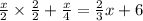
Second, Write each expression with a common denominator of 4, by multiplying each by appropriate factor of 1
Multiply
 and
and
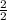
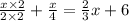
Multiply 2 and 2
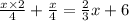
 Combine the numerators over the common denominator
Combine the numerators over the common denominator
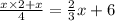
Third, Simplify the numerator
Move 2 to the left of x
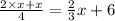
Add 2x and x
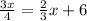
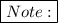 Combine
Combine
 and x
and x
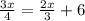
Fourth, Move all terms containing x to the left side of the equation
Subtract
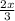 from both sides of the equation
from both sides of the equation
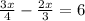
 To write
To write
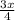 as a fraction with a common denominator, multiply by
as a fraction with a common denominator, multiply by


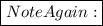 To write
To write
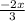 as a fraction with a common denominator, multiply by
as a fraction with a common denominator, multiply by


Fifth, Write each expression with a common denominator of 12, by multiplying each by an appropriate factor of 1
Multiply
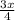 and
and

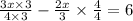
Multiply 4 and 3

Multiply
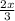 and
and

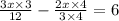
Multiply 3 and 4
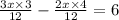
 Combine the numerators over the common denominator
Combine the numerators over the common denominator
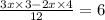
Sixth, Simplify the numerator
Factor x out of 3x ×3 - 2x × 4
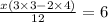
Multiply 3 by 3
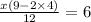
Multiply - 2 by 4

Subtract 8 from 9
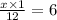
Multiply x by 1

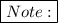 Multiply both sides of the equation by 12
Multiply both sides of the equation by 12
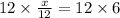
Seventh, Simplify both sides of the equation and cancel the common factor of 12
Cancel the common factor
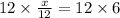
Rewrite the expression
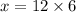
Lastly, Multiply 12 by 6
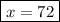
hope it's helps