raAnswer:
x = 5
Explanation:
Original equation =
 -
-
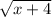 = 1
= 1
Remove square roots
 + 2x +1 = 4x +16
+ 2x +1 = 4x +16
Subtract 16 from both sides
 + 2x +1 = 4x +16
+ 2x +1 = 4x +16
-16 -16
---------------------------
 + 2x- 15= 4x
+ 2x- 15= 4x
Subtract 4x from both sides
 + 2x - 15 - 4x= 4x - 4x
+ 2x - 15 - 4x= 4x - 4x
=
 - 2x - 15 = 0
- 2x - 15 = 0
THIS EQUATION HAS 2 rational roots. {x1,x2} = {5,-3}
CHECK THAT THE FIRST SOLUTION IS CORRECT (5)
Original equation, root isolated, after tidy up
 =
=
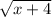
Plug in 5 for x
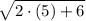 =
=
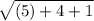
Simplify
 = 4
= 4
Solution checks !!
Solution is: x = 5
CHECK THAT THE SECOND SOLUTION IS CORRECT (-3)
Original equation, root isolated, after tidy up
 =
=
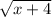
Plug in -3 for x
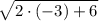 =
=

Simplify
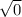 = 2
= 2
Solution does not check
0 ≠ 2
So, the answer is x = 5
Hope this helps!