Answer:
Part 1)
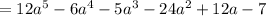
Part 2)

Explanation:
Part 1)
We would like to multiply:
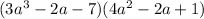
Distribute each term from the first group into the second group. So:
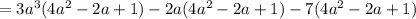
Distribute further:
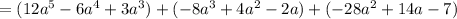
Combine like terms:
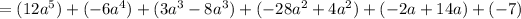
Simplify:
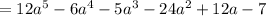
Part 2)
We would like to divide:
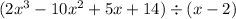
Using long division.
Please refer to the attached document.
For the first step, x goes into 2x³ 2x² times. Hence, we multiply our divisor by 2x².
Next, x goes into -6x^2 -6x times. Hence, we multiply our divisor by -6x.
Finally, x goes into -7x -7 times. So, we multiply our divisor by -7 and we simplify.
Therefore:
