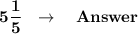Question

52/10 Convert to mixed numbers

Answer 1

`5 * (2)/(10)`

Explanation:

The number of times 10 can go in 52 will be the whole number

`5 * (?)/(?)`

10 will go in 52 5times which will be 50 remainder two.The remainder will be the numerator

`5 * (2)/(?)`

The denominator will be the original denominator (the number below)

`5 * (2)/(10)`

Answer 2

Reduce the expression 52/1 by eliminating common factors.

Factor 2 out of 52.

• 
  `\bf{(2(26))/(10) }`

Factor 2 out of 10.

• 
  `\bf{(2\cdot26)/(2\cdot5) }`

Cancel the common factor.

• 
  `\bf{\frac{\\ot{2}\cdot26}{\\ot{2}\cdot5} }`

Substitute the expression.

• 
  `\bf{(26)/(5) }`

Fit the division problem into long division format.

`\begin{matrix}\:\:\:\:\:\:\emptyspace5\:\:\:\:\:\:\:\:\:\:\:\\ 5\overline\:\:\:\:\:\:\:\:\:\\ \:\:\:\:\underline{\emptyspace2\emptyspace5}\:\:\:\:\:\:\:\:\:\:\:\:\\ \:\:\:\:\:\:\emptyspace1\emptyspace\:\:\:\:\:\:\:\:\:\:\end{matrix}`

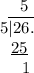
The result of the division 26/5 is 5 with a remainder of 1.

`\bf{5 \ r \ 1 }`

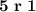
Use the long division solution to convert the original fraction,
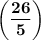`\bf{\left((26)/(5)\right) }` in a mixed number. The integer part of the mixed number will be the number of times the denominator of the original fraction integer divides the numerator of the original fraction, (5), and the fractional part of the mixed number will be the remainder of the original division (1) Enter the denominator of the original fraction, (5).

`\bf{5(1)/(5) \ \ \to \ \ \ Answer }`

`\huge \red{\boxed{\green{\boxed{\boldsymbol{\purple{Pisces04}}}}}}`