Answer:
8.7cm
Explanation:
Pythagorean Theorem
Pythagoras' Theorem deals with right triangles.
In a right triangle, the triangle has one right angle. The two sides of the triangle that are adjacent to the right angle are called legs, and the side across from the right angle is called a hypotenuse.
Pythagoras' Theorem states that the sum of the squares of the legs is equal to the square of the hypotenuse:
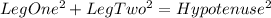
Recall that addition obeys the commutative property, meaning that 1+2 is the same as 2+1. This means that the side of the equation could be written as follows:
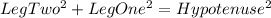
In other words, it doesn't matter which leg we call LegOne, and which leg we call LegTwo (but the Hypotenuse must be the side across from the right angle)
In the equation, the two legs are often simply labeled "a" & "b". Paired with the hypotenuse (often labeled "c"), the equation becomes:
Finding the Right Triangle
Observe that the red diagonal line, EG, cuts the rectangle into two congruent right-triangles (DEG & FGE). As the question asks us to find the length of the diagonal, and the Pythagorean Theorem uses a right triangle (not a rectangle), we'll need to focus on just on one of those two right triangles (there isn't an easy/hard one... it's the same process. I chose to focus on triangle FGE). Simultaneously, while focusing on that one triangle, we'll need to think about the properties of the rectangle as a whole.
Using the rectangle to find the parts of the triangle
Note that by definition, the rectangle has 4 congruent angles that are all right angles. Hence, angle F is a right angle, and thus triangle FGE is a right triangle (so we can apply the Pythagorean Theorem).
Since angle F is the right angle, EG is the Hypotenuse. The other two sides, FG and EF, are the legs.
In the diagram, we're given the length of leg FG.
Recall that rectangles are parallelograms, and consequently rectangles have two pairs of opposite congruent sides (the top and the bottom sides are the same length, and the left and the right sides are the same length). Hence, side EF also has a length of 6cm.
Using Pythagoras' Theorem
We can now begin by substituting known values into the equation, and then solving for the unknown:
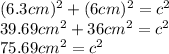
To solve for c, we would need to apply the Square Root Property.
Square Root Property: If
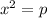, then
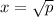or
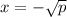
While the Square Root Property yields two separate answers (one positive; one negative), accepting that lengths of triangles are generally considered to be positive values, we exclude the negative result:
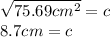
Note the final result is already rounded to 1 d.p., as requested by the question.