The software rendering this question really butchered it... I think it's saying the displacement vector for the particle is
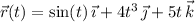
Differentiate twice with respect to time
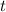 to get the velocity and acceleration vectors, respectively:
to get the velocity and acceleration vectors, respectively:
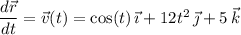
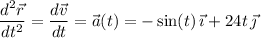
Then at
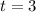 , the acceleration of the particle is
, the acceleration of the particle is
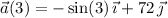
which most closely resembles the first choice.