Question

Which of the following could be the ratio between the lengths of the two legs

of a 30 60 90 triangle?
Check all that apply

Answer 1

E

Explanation:

Its simple

Answer 2

The correct option is e.

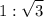`$1: √(3)$` is the only option that represents the correct ratio between the lengths of the two legs of a 30-60-90 triangle.

To determine which of the given ratios could represent the ratio between the lengths of the two legs of a 30-60-90 triangle, we need to recall that in such a triangle, the side lengths are in the ratio of 1:√3:2, where:

• The length of the side opposite the 30° angle is the shortest side, which we'll call "1 unit."
• The length of the side opposite the 60° angle is √3 times the length of the shortest side, so "√3 units."
• The length of the side opposite the 90° angle (the hypotenuse) is twice the length of the shortest side, so "2 units."

We're interested in the ratio between the lengths of the two legs, not the hypotenuse. This means we're looking for a ratio that can simplify to 1:√3 or its equivalent.

Let's evaluate each option:

A.
`\( √(2) : √(2) \)` simplifies to 1:1, which is not the correct ratio for the legs of a 30-60-90 triangle.

B.
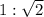`\( 1 : √(2) \)` is not the correct ratio either, since we expect a ratio of 1:√3 for the two legs.

C.
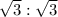`\( √(3) : √(3) \)` simplifies to 1:1, which, like option A, is not correct for a 30-60-90 triangle.

D.
`\( √(2) : √(3) \)` is not the ratio of the two legs of a 30-60-90 triangle.

E.
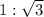`\( 1 : √(3) \)` is the correct ratio for the legs of a 30-60-90 triangle, with the shorter leg having a length of 1 unit and the longer leg having a length of √3 units.

F.
`\( √(3) : 3 \)` can be simplified to
`\( (√(3))/(3) \)`, which simplifies further to
`\( (1)/(√(3)) \)` when multiplied by
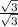`\( (√(3))/(√(3)) \)`, resulting in
`\( (√(3))/(3) \)`. This is not the ratio of the two legs of a 30-60-90 triangle either.

So the correct answer is
`\( 1 : √(3) \)`.

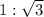The complete question is here: