Answer:
a) The average rate of change for the function
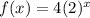 over interval x=1 to x=2 is 8
over interval x=1 to x=2 is 8
b) The average rate of change for the function
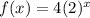 over interval x=3 to x=4 is 32
over interval x=3 to x=4 is 32
Explanation:
We are given function
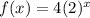
We need to find Average rate of change
The formula used is:
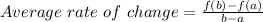
Part a) The interval is: x=1 to x=2
We have a= 1 and b=2
Finding f(a) i.e f(1)
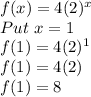
Now finding f(b) i.e f(2)
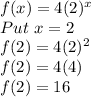
Now finding average rate of change.
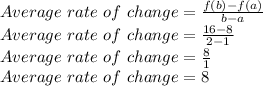
So, average rate of change for the function
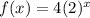 over interval x=1 to x=2 is 8
over interval x=1 to x=2 is 8
Part b)
The interval is: x=3 to x=4
We have a= 3 and b=24
Finding f(a) i.e f(3)
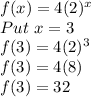
Now finding f(b) i.e f(4)
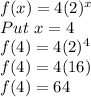
Now finding average rate of change.
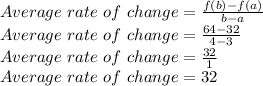
So, average rate of change for the function
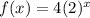 over interval x=3 to x=4 is 32
over interval x=3 to x=4 is 32
Since the interval is increasing, so does our average rate of change increasing as function is also increasing.