Question

HELP A line passes through two points with coordinates (6,-8) and (-3,7).

Drag numbers to the lines to represent the equation of the line in standard form.

Answer 1

3y+5x=6

Explanation:

Equation of the Line

The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

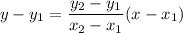
The line passes through the points (6,-8) and (-3,7), thus:

`\displaystyle y+8=(7+8)/(-3-6)(x-6)`

`\displaystyle y+8=(15)/(-9)(x-6)`

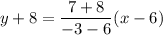
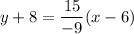
Simplifying:

`\displaystyle y+8=-(5)/(3)(x-6)`

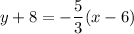
Multiplying by 3:

`3(y+8)=-5(x-6)`

`3y+24=-5x+30`

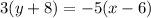
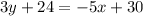
Moving all the variables to the left side:

3y + 5x = 30 - 24

3y + 5x = 6