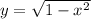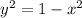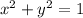Answer:
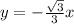

Explanation:
You are correct with the graph, the angle
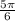
should lies in the second quadrant so the polar graph will lie in the second quadrant then go to the fourth quadrant. It would be a line not a circle.
For the equation, use the tangent equation because it has y and x in it
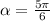
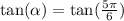
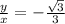
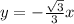
For the next picture, the graph is correct,
We know that
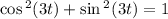

Alternate Way:
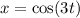

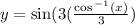

Here we must imagine a triangle such that an angle has a hypotenuse 1, and a leg x, by definition the missing side is

by using the Pythagorean theorem.
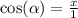
so